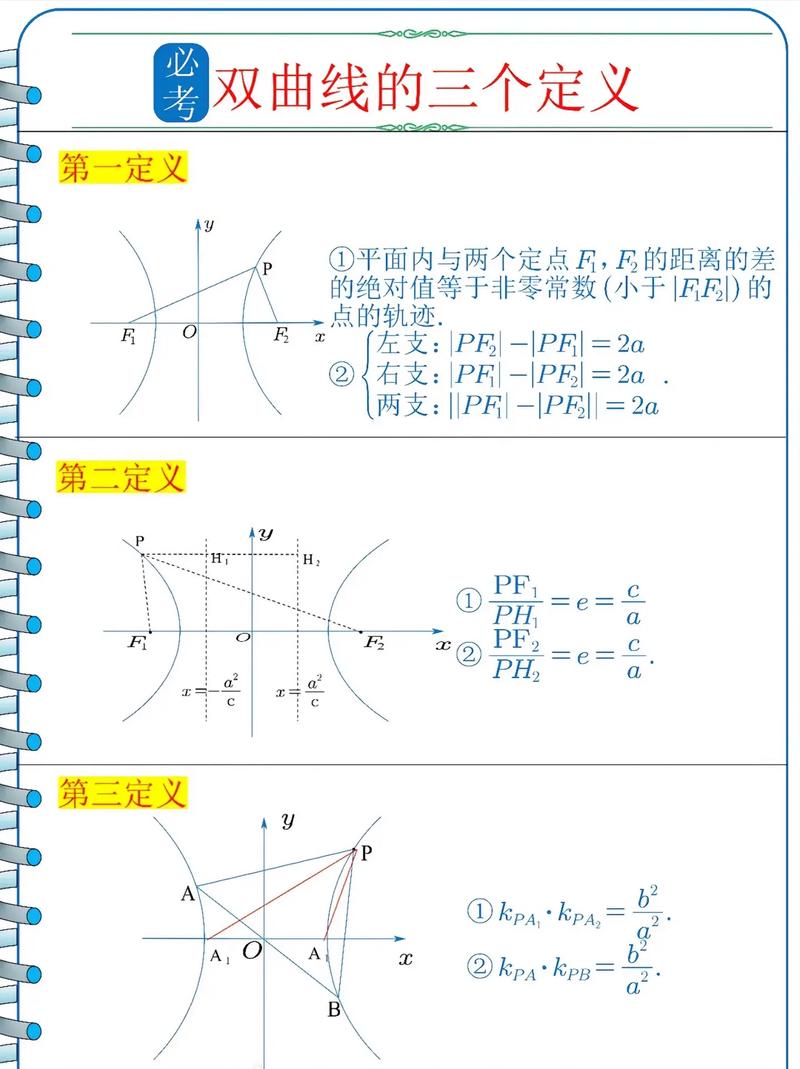
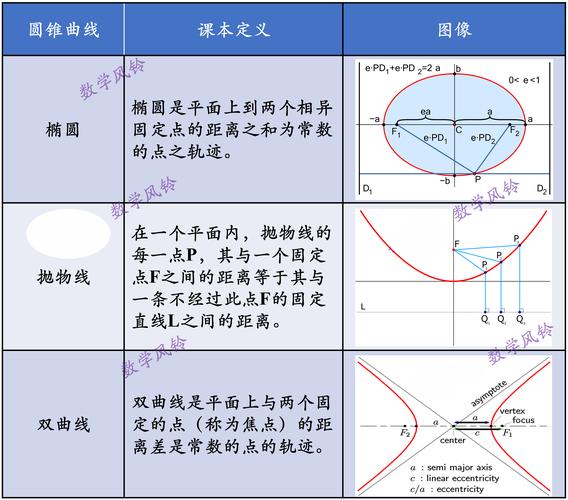
本篇文章给大家谈谈空间曲线怎样定义,以及空间曲线的定义对应的知识点,希望对各位有所帮助,不要忘了收藏本站喔。
3.给出:曲线,闭曲线,曲面,闭曲面的定义
一维单连通:在内部随便画一条!封闭!曲线,然后不断缩短它,如果最后都能缩成一个点,就是一维单连通。环面(轮胎内胆)就不是,因为如果画一个圈不断缩短,会碰上中间的洞,而球面就可以一直缩啊缩,不会有洞挡着。二维单连通:在内部随便画一个!封闭!曲面,然后不断缩小,最后都能缩成一个点,就是二维单连通。
(图片来源网络,侵删)
定义闭区域:由一个开集及其边界构成的***。闭区域包括边界上的所有点。 闭区域的特征:闭区域是由一条或多条闭合的曲线(简单闭曲线)及其内部组成的平面区域。在三维空间中,这一概念类比到由闭合曲面及其内部构成的空间区域。
它总是非空的。内部的补集称为边界;它是一个流形,或者说闭曲线的并集。无边界的曲面称为闭的,如果它是紧compact的,否则称为开。--- 所以闭曲面2大特性:紧和无边界,只有极限。
什么叫空间曲线
空间曲线是经典微分几何的主要研究对象之一,在直观上曲线可看成空间一个自由度的质点运动的轨迹。研究空间曲线的有力工具是微积分,我们可以用微积分来推导三个刻划一条空间曲线几何性质的基本几何量,就是弧长、曲率和挠率。我们所接触到的空间,大至宇宙,小至细胞,其中都充满着五光十色、变幻纷杂的曲线。
(图片来源网络,侵删)
空间曲线是存在于三维空间中的曲线,其定义方式有多种。曲面相交:空间曲线可以由两个曲面相交得到。在这种情况下,空间曲线的解析式可以通过联立两个曲面的方程来确定。
空间曲线是指两个曲面相交得到的曲线,或者如螺旋线等使用参数方程更方便表示的曲线。以下是关于空间曲线的详细定义和解释:定义:曲面相交:空间曲线可以由两个曲面相交得到,其解析式可以通过联立这两个曲面的方程来确定。
空间曲线怎样定义
空间曲线是空间中满足一定条件的点的轨迹,其定义可以从以下几个方面来理解:曲面相交定义 空间曲线可以由两个曲面相交得到。当两个曲面在空间中有公共部分时,这些公共部分往往形成一条或多条空间曲线。此时,空间曲线的解析式可以通过联立这两个曲面的方程来确定。
(图片来源网络,侵删)
空间曲线的定义如下:空间曲线是存在于三维空间中的曲线,其定义方式有多种。曲面相交:空间曲线可以由两个曲面相交得到。在这种情况下,空间曲线的解析式可以通过联立两个曲面的方程来确定。
空间曲线是指两个曲面相交得到的曲线,或者如螺旋线等使用参数方程更方便表示的曲线。以下是关于空间曲线的详细定义和解释:定义:曲面相交:空间曲线可以由两个曲面相交得到,其解析式可以通过联立这两个曲面的方程来确定。
空间曲线的定义:两个曲面相交可以得到空间曲线,而且其解析式可以用两个曲面的方程联立方程组来确定。但空间曲线可并非全部是两个曲面相交可以得到,比如螺旋线,他的方程使用参数方程表示就更方便。
空间曲线怎样定义的介绍就聊到这里吧,感谢你花时间阅读本站内容,更多关于空间曲线的定义、空间曲线怎样定义的信息别忘了在本站进行查找喔。
本文可能通过AI自动登载或用户投稿,文章仅代表原作者个人观点。本站旨在传播优质文章,无商业用途。如侵犯您的合法权益请联系删除。