今天给各位分享抛物线的焦半径的公式是怎么来的的知识,其中也会对抛物线的焦半径公式及其推导进行解释,如果能碰巧解决你现在面临的问题,别忘了关注本站,现在开始吧!
抛物线焦半径推导
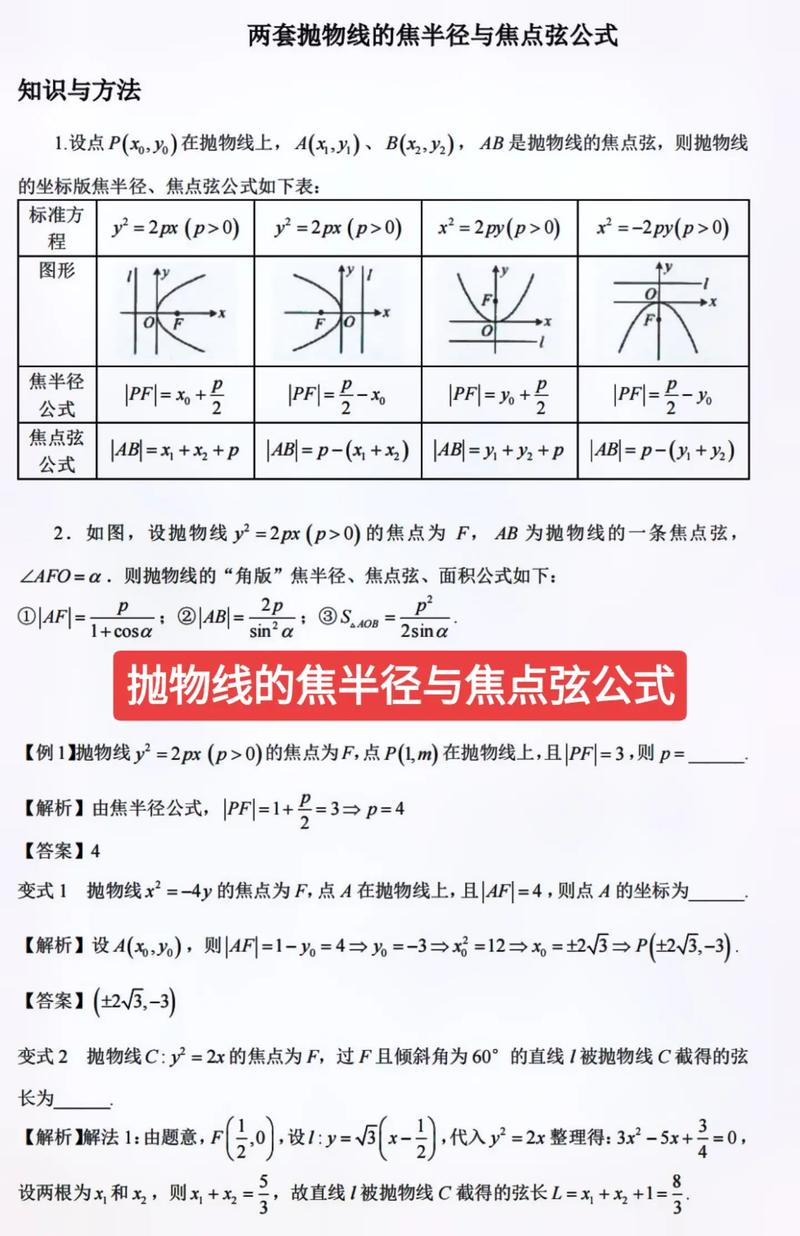
抛物线焦半径公式推导为:抛物线r=x+p/2。抛物线的焦半径是连接抛物线上的点与对应的焦点的线段。焦半径公式的推导为抛物线r=x+p/2。
(图片来源网络,侵删)
抛物线焦半径推导公式:(y2=2px(p0)|MF|=2x0M(x0,y0)为抛物线上任意一点的坐标。当平面与二次锥面的母线平行,且不过圆锥顶点,结果为抛物线。当平面与二次锥面的母线平行,且过圆锥顶点,结果退化为一条直线。当平面只与二次锥面一侧相交,且不过圆锥顶点,结果为椭圆。
抛物线的焦半径公式跟角度是有关的。分析:抛物线方程为y^2=2px(p0),即开口向右时,焦半径r=x+p/2;当抛物线方程为y^2=-2px,即开口向左时,焦半径r=-x+p/2;当抛物线方程为x^=2px,即开口向上时,焦半径r=y+p/2;当抛物线方程为x^=-2px,即开口向下时,焦半径r=-y+p/2。
焦半径公式的推导: 利用双曲线的第二定义:设双曲线 , 是其左右焦点。 则由第二定义: , 同理: 即有焦点在x轴上的双曲线的焦半径公式: 同理有焦点在y轴上的双曲线的焦半径公式: ( 其中 分别是双曲线的下上焦点)。
(图片来源网络,侵删)
抛物线的焦半径公式是怎样推导的?
1、抛物线焦半径公式推导为:抛物线r=x+p/2。抛物线的焦半径是连接抛物线上的点与对应的焦点的线段。焦半径公式的推导为抛物线r=x+p/2。
2、抛物线焦半径推导公式:(y2=2px(p0)|MF|=2x0M(x0,y0)为抛物线上任意一点的坐标。当平面与二次锥面的母线平行,且不过圆锥顶点,结果为抛物线。当平面与二次锥面的母线平行,且过圆锥顶点,结果退化为一条直线。当平面只与二次锥面一侧相交,且不过圆锥顶点,结果为椭圆。
3、如下:焦半径公式的推导: 利用双曲线的第二定义:设双曲线 , 是其左右焦点。 则由第二定义: , 同理: 即有焦点在x轴上的双曲线的焦半径公式: 同理有焦点在y轴上的双曲线的焦半径公式: ( 其中 分别是双曲线的下上焦点)。
(图片来源网络,侵删)
4、抛物线y^2=2px (p0),C(Xo,Yo)为抛物线上的一点,焦半径|CF|=Xo+p/2。焦半径r=x+p/2 (其中x为在抛物线上的横坐标,p为焦准距) (利用抛物线第二定义求),至于抛物线开口方向为其他三个方向时,利用抛物线第二定义求同理可求。
5、焦半径公式:对于抛物线 $y^2 = 2px$ 上的点 $A(x_0, y_0)$,其焦半径 $|AF|$ 可以表示为:|AF| = x_0 + frac{p}{2} 这个公式是基于抛物线的定义得出的,即抛物线上的点到焦点的距离等于到准线的距离。
高中数学:抛物线的焦半径公式怎么来的?
1、圆锥曲线上任意一点M与圆锥曲线焦点的连线段,叫做圆锥曲线焦半径。圆锥曲线上一点到焦点的距离,不是定值。焦半径:曲线上任意一点与焦点的连线段焦点弦,过一个焦点的弦通径。过焦点并垂直于轴的弦圆锥曲线(除圆外)中,过焦点并垂直于轴的弦。
2、抛物线焦半径推导公式:(y2=2px(p0)|MF|=2x0M(x0,y0)为抛物线上任意一点的坐标。当平面与二次锥面的母线平行,且不过圆锥顶点,结果为抛物线。当平面与二次锥面的母线平行,且过圆锥顶点,结果退化为一条直线。当平面只与二次锥面一侧相交,且不过圆锥顶点,结果为椭圆。
3、抛物线焦半径公式推导为:抛物线r=x+p/2。抛物线的焦半径是连接抛物线上的点与对应的焦点的线段。焦半径公式的推导为抛物线r=x+p/2。
抛物线的焦半径公式
抛物线焦半径的四个公式如下:对于开口向右或向左的抛物线:当点P在x轴上方时,焦半径公式为:|PF|=x0+p/2 当点P在x轴下方时,焦半径公式为:|PF|=x0+p/2 对于开口向上或向下的抛物线:当点P在y轴右侧时,焦半径公式为:|PF|=y0+p/2 当点P在y轴左侧时,焦半径公式为:|PF|=y0+p/2 其中,是抛物线上任意一点M的坐标,p是抛物线的焦距。
抛物线焦半径公式推导为:抛物线r=x+p/2。抛物线的焦半径是连接抛物线上的点与对应的焦点的线段。焦半径公式的推导为抛物线r=x+p/2。
抛物线y^2=2px (p0),C(Xo,Yo)为抛物线上的一点,焦半径|CF|=Xo+p/2。焦半径r=x+p/2 (其中x为在抛物线上的横坐标,p为焦准距) (利用抛物线第二定义求),至于抛物线开口方向为其他三个方向时,利用抛物线第二定义求同理可求。
抛物线的焦半径公式 对于抛物线 $y^2 = 2px$(其中 $p 0$),其焦点为 $F(frac{p}{2}, 0)$,准线方程为 $x = -frac{p}{2}$。抛物线上的任意一点 $A(x_0, y_0)$ 到焦点 $F$ 的距离 $|AF|$ 称为焦半径。
焦半径公式的抛物线的焦半径公式为:R = 2p,其中p为抛物线的焦距。详细解释如下:在几何学中,抛物线是一种特殊的二次曲线,具有一个焦点和一个与之对称的准线。对于抛物线而言,焦半径是指从焦点到曲线上任意一点的距离。对于标准形式的抛物线方程,其焦半径的公式为R = 2p。
抛物线的焦半径公式是什么,如何求解?
抛物线y^2=2px (p0),C(Xo,Yo)为抛物线上的一点,焦半径|CF|=Xo+p/2。焦半径r=x+p/2 (其中x为在抛物线上的横坐标,p为焦准距) (利用抛物线第二定义求),至于抛物线开口方向为其他三个方向时,利用抛物线第二定义求同理可求。如果焦点不在坐标轴上,只需要将x进行相应平移即可,p不变。
抛物线的焦半径是r=x+p/2。抛物线是指平面内到一个定点F(焦点)和一条定直线l(准线)距离相等的点的轨迹。它有许多表示方法,例如参数表示,标准方程表示等等。曲线上任意一点M与曲线焦点的连线段,叫做抛物线的焦半径。曲线上一点到焦点的距离,不是定值。
抛物线的焦半径公式是描述抛物线上任意一点到焦点距离的重要工具。对于标准形式的抛物线 $y^2 = 2px$ 或 $y^2 = -2px$,焦半径公式可以简化为 $x_0 + frac{p}{2}$ 或 $-x_0 - frac{p}{2}$(注意 $x_0$ 的取值范围)。
对于抛物线 $y^2 = 2px$(其中 $p 0$),其焦点为 $F(frac{p}{2}, 0)$,准线方程为 $x = -frac{p}{2}$。抛物线上的任意一点 $A(x_0, y_0)$ 到焦点 $F$ 的距离 $|AF|$ 称为焦半径。
求抛物线上某点到焦点的距离:直接利用焦半径公式或定义法求解。判断抛物线上某点与焦点的位置关系:通过比较焦半径的大小来判断。解决与抛物线焦点、准线相关的几何问题:利用焦半径与准线的性质进行求解。
抛物线焦半径公式cos推导过程是怎么样的?
1、焦半径公式的推导: 利用双曲线的第二定义:设双曲线 , 是其左右焦点。 则由第二定义: , 同理: 即有焦点在x轴上的双曲线的焦半径公式: 同理有焦点在y轴上的双曲线的焦半径公式: ( 其中 分别是双曲线的下上焦点)。
2、抛物线焦半径公式推导为:抛物线r=x+p/2。抛物线的焦半径是连接抛物线上的点与对应的焦点的线段。焦半径公式的推导为抛物线r=x+p/2。
3、对于抛物线 $y^2 = 2px$(其中 $p 0$),其焦点为 $F(frac{p}{2}, 0)$,准线方程为 $x = -frac{p}{2}$。抛物线上的任意一点 $A(x_0, y_0)$ 到焦点 $F$ 的距离 $|AF|$ 称为焦半径。
4、抛物线焦半径推导公式:(y2=2px(p0)|MF|=2x0M(x0,y0)为抛物线上任意一点的坐标。当平面与二次锥面的母线平行,且不过圆锥顶点,结果为抛物线。当平面与二次锥面的母线平行,且过圆锥顶点,结果退化为一条直线。当平面只与二次锥面一侧相交,且不过圆锥顶点,结果为椭圆。
5、|=a+es。|TF_2|=a-ex。(其中F_F_2为左、右焦点,以下均同)。
6、特殊情况下的焦半径公式:在题目给出的特定情况下,即抛物线与斜率为 $tantheta$ 的直线相交于 $A, B$ 两点时,我们可以利用几何关系推导出焦半径 $|AF|$ 和 $|BF|$ 的另一种表达式。
抛物线的焦半径的公式是怎么来的的介绍就聊到这里吧,感谢你花时间阅读本站内容,更多关于抛物线的焦半径公式及其推导、抛物线的焦半径的公式是怎么来的的信息别忘了在本站进行查找喔。
本文可能通过AI自动登载或用户投稿,文章仅代表原作者个人观点。本站旨在传播优质文章,无商业用途。如侵犯您的合法权益请联系删除。