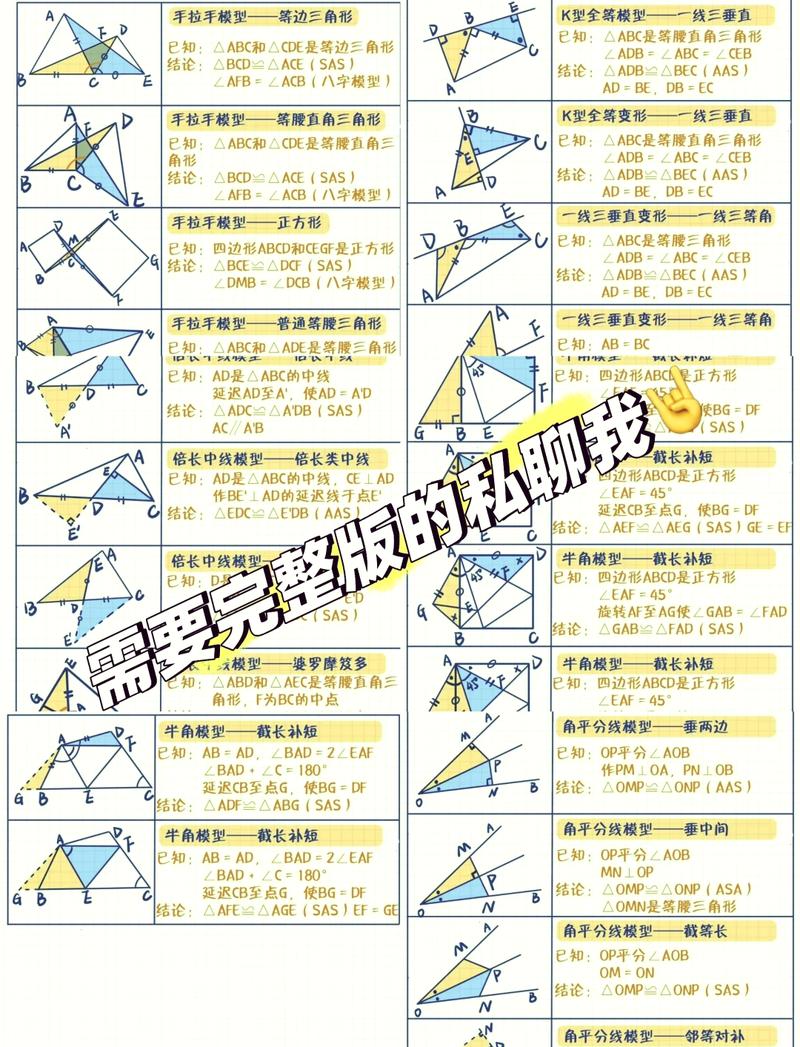
本篇文章给大家谈谈全等三角形怎么算法,以及全等三角形的步骤怎么写对应的知识点,希望对各位有所帮助,不要忘了收藏本站喔。
证三角形全等有几种方法
目前证明两个三角形全等,共有以下四种方法:边角边(SAS):保证两组对应边分别相等,并且这两组对应边的夹角也相等,就可以确保画出的三角形和原三角形全等。例如,已知三角形ABC和三角形ABC,若AB = AB,AC = AC,且∠A = ∠A,那么△ABC ≌ △ABC。
(图片来源网络,侵删)
证明全等三角形的方法主要有以下几种:对于普通三角形:边角边(S.A.S):如果两个三角形的两边及它们之间的夹角分别对应相等,则这两个三角形全等。角边角(A.S.A):如果两个三角形的两角及它们之间的夹边分别对应相等,则这两个三角形全等。
一共有六种全等的判定方法,分别是 边边边(SSS):三条边对应相等的两个三角形全等。边角边(SAS):两条边和它们的夹角对应相等的两三角形全等。角角边(AAS):两个角和一条边对应相等的两三角形全等。角边角(ASA):两个角和它们的夹边对应相等的两三角形全等。
全等证明常用的五种方法包括SSS法、SAS法、ASA法、AAS法和HL法。每种方法都有其适用的条件和步骤,通过比较边长和角度的相等性来推导图形的全等关系。这些方法在几何学证明中有广泛应用,帮助我们理解和证明图形的全等性质。全等介绍 三角形全等是指两个三角形的对应的三条边和对应的三个角完全相等。
(图片来源网络,侵删)
证明全等三角形的方法主要有以下几种:对于普通三角形:边角边(S.A.S):定义:如果两个三角形的两边及它们之间的夹角分别对应相等,则这两个三角形全等。应用:此方法适用于已知两边长度和它们之间夹角的情况。
全等三角形的判定方法有哪五种?
SSS(Side-Side-Side)(边边边):三边对应相等的三角形是全等三角形。SAS(Side-Angle-Side)(边角边):两边及其夹角对应相等的三角形是全等三角形。ASA(Angle-Side-Angle)(角边角):两角及其夹边对应相等的三角形全等。
全等三角形的判定方法有五种,分别是:SSS全等判定:当两个三角形的三边长度都相等时,这两个三角形全等。SAS全等判定:当两个三角形中,两边长度相等并且这两边所夹的角也相等时,这两个三角形全等。AAS全等判定:当两个三角形中,有两个角及它们的夹边对应相等时,这两个三角形全等。
(图片来源网络,侵删)
三角形全等的判定方法有以下五种:SSS判定法:定义:当两个三角形的三边长度完全相等时,这两个三角形全等。SAS判定法:定义:如果两个三角形的两边长度相等,且这两边所夹的角也相等,那么这两个三角形全等。
全等三角形的判定方法有以下五种:边边边:定义:三边对应相等的两个三角形全等。说明:如果两个三角形的三边分别相等,则这两个三角形全等。边角边:定义:两边和它们夹角对应相等的两个三角形全等。说明:如果两个三角形的两边及它们之间的夹角分别相等,则这两个三角形全等。
全等三角形的五种判定方法如下: 边边边全等(SSS):当两个三角形的三条边分别相等时,这两个三角形全等。这是判定全等三角形最基础的准则。 边角边全等(SAS):如果两个三角形中有两边及其夹角分别相等,则这两个三角形全等。
全等三角形的判定方法有以下五种:SSS全等判定法:当两个三角形的三边对应相等时,这两个三角形全等。三条边确定了一个三角形的形状和大小。SAS全等判定法:当两个三角形的两边及其夹角对应相等时,这两个三角形全等。夹角是两个相邻边所夹的角,这种判定方法基于形状和大小相似的原则。
如何判定三角形全等?
SSS(Side-Side-Side)判定法:如果两个三角形的三条边分别相等,则这两个三角形全等。 SAS(Side-Angle-Side)判定法:如果两个三角形中有两边和它们之间的夹角分别相等,则这两个三角形全等。
全等三角形的判定方法有以下五种:边边边:定义:三边对应相等的两个三角形全等。说明:如果两个三角形的三边分别相等,则这两个三角形全等。边角边:定义:两边和它们夹角对应相等的两个三角形全等。说明:如果两个三角形的两边及它们之间的夹角分别相等,则这两个三角形全等。
角角全等(AAS):如果两个三角形中有两个角分别相等,且这两个角所夹的边也相等,则这两个三角形全等。 直角三角形中的HL:在直角三角形中,如果一条直角边和斜边分别相等,则这两个直角三角形全等。这一判定方法也称为HL判定。
全等三角形的判定方法:“边边边”、“边角边”、“角边角”、“角角边”、“直角、斜边、边”。SSS(边边边),当三角形的三边对应相等时那么这两个三角形是全等三角形。SAS(边角边),两边及其夹角对应相等的三角形是全等三角形。ASA(角边角),两角及其夹边对应相等的三角形全等。
边角边(SAS):各三角形的其中两条边的长度都对应相等,且这两条边的夹角(即这两条边组成的角)都对应相等的话,该两个三角形就是全等三角形。角边角(ASA):两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。
判定三角形全等有五种方法哦:边边边:如果两个三角形的三边分别相等,那么这两个三角形就是全等的。简单说,就是三条边都一样长啦!边角边:这个方法需要两个三角形的两边及它们之间的夹角分别相等。
怎样用几何方法证明三角形全等?
SSS(边边边)即三边对应相等的两个三角形全等。SAS(边角边)即三角形的其中两条边对应相等,且两条边的夹角也对应相等的两个三角形全等。ASA(角边角)即三角形的其中两个角对应相等,且两个角夹边也对应相等的两个三角形全等。AAS(角角边)即三角形的其中两个角对应相等,且对应相等的角所对应的边也对应相等的两个三角形全等。
直线是可以向两边无限延伸的;过两点有且只有一条直线;平面内过一点可以任何半径画圆;两直线平行,同位角相等;等量+等量和相等;等量-等量,其差相等;能重合的图形全等;整体大于部分。除了上面列出的,都不是公理。
答案:翻折法是通过将图形的一部分沿着某条直线翻折,使得翻折前后的两部分完全重合,从而构造出全等三角形。这种方法常用于证明线段相等或角相等。示例:在证明等腰三角形的性质时,可以沿等腰三角形的底边中线翻折,得到两个全等的直角三角形。
三角形证全等的方法
那么这两个三角形全等。这是由于角确定了一条边的情况下再增加一个相同的角便能保证两边可以构成一个封闭的几何形状,即三角形。以上五个判定方法均基于三角形的几何特性,通过不同的组合方式来确定三角形的全等关系。在实际应用中可以根据具体情况选择合适的判定方法来进行证明或计算。
ASA(角边角):两角及其夹边对应相等的三角形全等。AAS(角角边):两角及其一角的对边对应相等的三角形全等。RHS(Right angle-Hypotenuse-Side)(直角、斜边、边)(又称HL定理(斜边、直角边):在一对直角三角形中,斜边及另一条直角边相等。
因为“边边角”证明三角形全等是一个假命题,存在反例,反例如下:边边角的两个三角形不一定全等,如下图所示:在数学中,全等一般是指全等三角形。全等三角形是指两个形状相同的三角形。全等三角形的对应角相等、对应边相等。
只要证明出,两个三角形,三边相等或者三角相等就可以了。没有顺序要求。三角形全等有五种判别方法:SSS,即边边边。三边对应相等的三角形是全等三角形。SAS,即边角边。两边及其夹角对应相等的三角形是全等三角形。ASA,即角边角。两角及其夹边对应相等的三角形全等。AAS,即角角边。
如果两个直角三角形的三边长度分别相等,那么这两个直角三角形全等。HL判定:这是直角三角形特有的一种全等判定方法。如果两个直角三角形的斜边和一个直角边分别相等,那么这两个直角三角形全等。在使用这些判定方法时,需要根据题目给出的条件,灵活选择适合的判定定理来证明两个直角三角形是否全等。
ASA(Angle-Side-Angle)(角边角):两角及其夹边对应相等的三角形全等。AAS(Angle-Angle-Side)(角角边):两角及其一角的对边对应相等的三角形全等。
全等三角形怎么算法的介绍就聊到这里吧,感谢你花时间阅读本站内容,更多关于全等三角形的步骤怎么写、全等三角形怎么算法的信息别忘了在本站进行查找喔。
本文可能通过AI自动登载或用户投稿,文章仅代表原作者个人观点。本站旨在传播优质文章,无商业用途。如侵犯您的合法权益请联系删除。