本篇文章给大家谈谈动态规划的基本思想和原理,以及动态规划的基本思想和原理是什么对应的知识点,希望对各位有所帮助,不要忘了收藏本站喔。
用动态规划解决矩阵链乘法问题时,最优子结构问题是什么
1、两种重要算法思想: 动态规划,贪心算法 动态规划:基本原理:动态规划英文名dynamic programming。其中pogramming指的是表格法,而非编写计算机程序。
(图片来源网络,侵删)
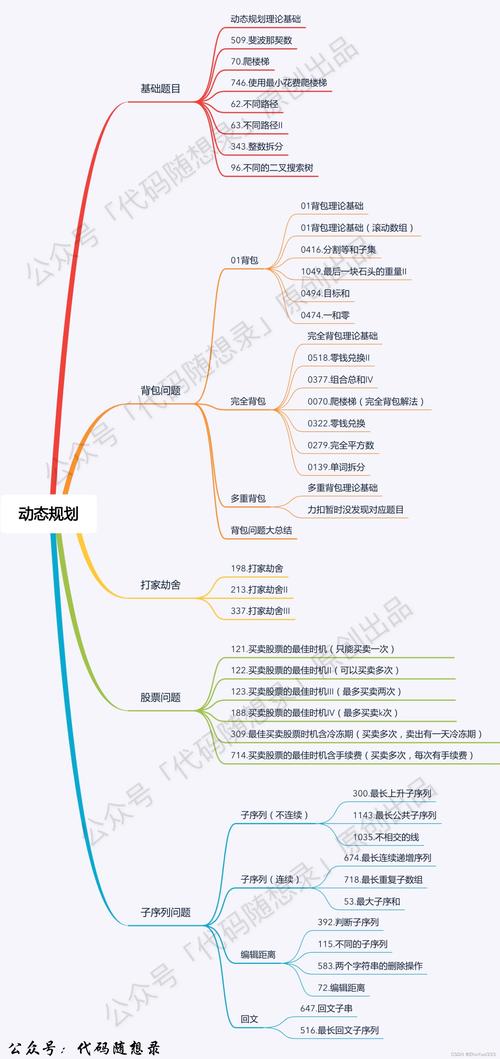
2、动态规划的适用场景动态规划适用于问题可分解为重叠子问题、且存在最优子结构(即全局最优解包含子问题最优解)的情况。除“小偷偷房子”问题外,还广泛应用于背包问题、最长公共子序列、矩阵链乘法等领域。其优势在于通过存储子问题解(如dp数组)避免重复计算,显著提升效率。
3、DP是动态规划的缩写,是一种解决问题的算法思想。以下是关于DP的详细解释:核心思想:DP通过将原问题分解为若干子问题,逐步求解得出最优解。优点:减少计算量:通过存储和复用子问题的解,避免重复计算,提高程序效率。
算法分析中动态规划的四个基本步骤?
描述最优解的结构特征。 递归地定义一个最优解的值。 自底向上计算一个最优解的值。 从已计算的信息中构造一个最优解。基本概念 动态规划过程涉及每次决策都依赖于当前状态,并随之引起状态的转移。决策序列是在不同状态中逐步形成的,因此,这种分阶段的优化决策过程被称为动态规划。
(图片来源网络,侵删)
描述优解的结构特征。递归地定义一个最优解的值。自底向上计算一个最优解的值。从已计算的信息中构造一个最优解。基本概念 动态规划过程是:每次决策依赖于当前状态,又随即引起状态的转移。
分解:将n个元素分成各含n/2个元素的子序列。解决:用合并排序法对两个子序列递归地排序。合并:合并两个已排序的子序列以得到排序结果。动态规划法 动态规划算法的设计可以分为如下四个步骤:描述最优解的结构。递归定义最优解的值。按自底向上的方式计算最优解的值。
动态规划算法的基本思想
动态规划算法的基本思想是将大问题分解为若干子问题,通过求解子问题并组合其解来得到原问题的解,以此逐步获取最优解。该算法通常用于求解具有最优性质的问题,这类问题存在多个可行解,我们旨在找出具有最优值的解。在将大问题分解成子问题时,这些子问题往往并非相互独立,若使用分治法求解,会产生大量重复计算的子问题。
(图片来源网络,侵删)
动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题。但是经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。在用分治法求解时,有些子问题被重复计算了许多次。
综上所述,动态规划是一种通过分解问题、存储子问题解并重用这些解来高效求解复杂问题的方法。其核心思想在于利用问题的最优子结构、无后效性和子问题重叠性质来减少重复计算和提高算法效率。
动态规划的基本思想是将待求解问题分解成若干个子问题,并保存已解决的子问题的答案,以避免大量重复计算。具体来说:问题分解:动态规划算法将待求解的问题分解成若干个子问题。这些子问题之间往往存在依赖关系,与分治法不同,分治法分解的子问题通常是相互独立的。
动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。
动态规划的基本思想和原理的介绍就聊到这里吧,感谢你花时间阅读本站内容,更多关于动态规划的基本思想和原理是什么、动态规划的基本思想和原理的信息别忘了在本站进行查找喔。
本文可能通过AI自动登载或用户投稿,文章仅代表原作者个人观点。本站旨在传播优质文章,无商业用途。如侵犯您的合法权益请联系删除。