本篇文章给大家谈谈假分数怎么化成带分数的过程,以及假分数如何化成带分数过程对应的知识点,希望对各位有所帮助,不要忘了收藏本站喔。
假分数与带分数怎样转换?
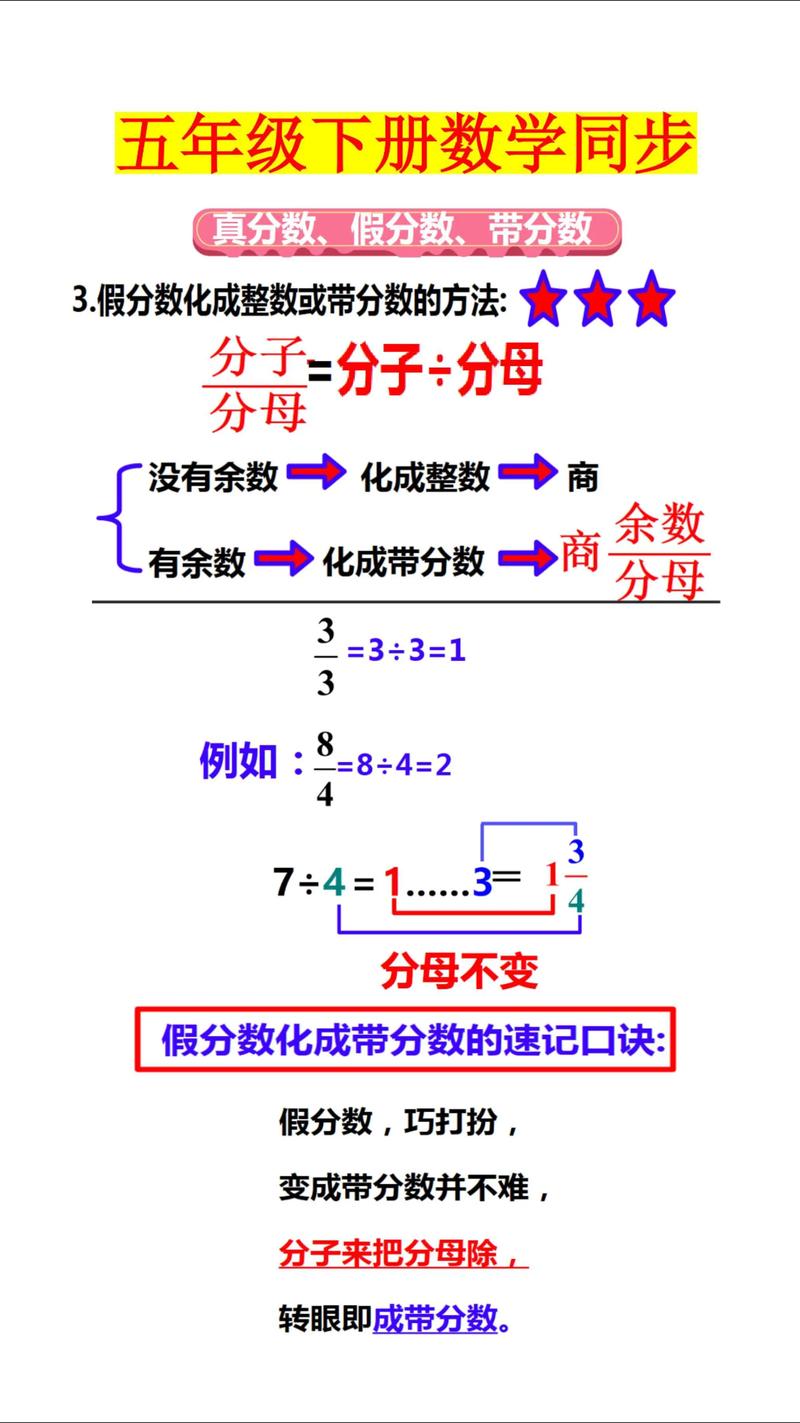
带分数和假分数之间可以通过互化进行转换。下面是具体的方法:假分数转换为带分数:假分数是指分子大于分母的分数,例如:7/4。将假分数转换为带分数的方法是将分子除以分母得到整数部分,余数作为新的分子,分母保持不变。例如,7/4可以转换为1 3/4。
(图片来源网络,侵删)
除法运算:首先,用假分数的分子除以分母。确定整数部分:所得的商即为带分数的整数部分。确定新的分子:除法运算中的余数将作为带分数的新分子。分母保持不变:带分数的分母与假分数的分母相同。示例:假设有一个假分数 $frac{10}{3}$,按照上述步骤进行转换: 用10除以3,商为3,余数为1。
假分数化带分数:把假分数化成整数或带分数,要用分子除以分母:能整除的,所得的商就是整数;不能整除的,商就是带分数的整数部分,余数就是分数部分的分子,分母不变。带分数注意:带分数的分数部分不能是假分数。带分数与字母相乘时要写成假分数的形式。
把带分数化成假分数,需要用原来的分母作为分母,将分与带分数的整数部分的乘积加上原来的分子作为假分数的分子。 带分数的概念 带分数由整数和真分数组成。
(图片来源网络,侵删)
假分数转化为带分数的方法是通过乘法运算。例如,将假分数 7/4 转化为带分数,可以将分子 7 乘以分母 4,得到商 1 余 3。因此,7/4 可以表示为 1 3/4。 带分数转化为假分数的方法是通过除法运算。
要将假分数转换为带分数,你可以按照以下步骤进行操作:首先,将分子除以分母,得到一个整数商和余数。例如,对于假分数7/4,7除以4的商为1余数为3。 将商作为带分数的整数部分。在这个例子中,商为1,所以带分数的整数部分为1。将余数作为带分数的分子部分。
假分数化带分数怎样化?
假设有一个假分数7/3,将7除以3得到商2余1。因此,带分数的整数部分是2,分数部分是1/3。所以,假分数7/3化为带分数是2又1/3。通过上述步骤,可以将任何假分数转化为带分数的形式。
(图片来源网络,侵删)
把假分数化成带分数的方法如下:用分子除以分母: 首先,确定假分数的分子和分母。 然后,用分子除以分母。所得的商做带分数的整数部分: 除法的结果中,商即为带分数的整数部分。余数做分子,分母不变: 除法结果中的余数,将作为新的分数的分子,而分母保持不变。
把假分数化成带分数的方法是:用分子除以分母,所得的商做带分数的整数部分,余数做新的分子,分母保持不变。具体步骤如下:确定假分数:首先确认给定的分数是否为假分数,即分子是否大于或等于分母。进行除法运算:将假分数的分子除以分母。
假分数化带分数的步骤:找出假分数的最简形式。即,通过约分,将假分数化成不能再简化的形式。确定假分数的分子和分母。假分数的分子是整数和真分数的分子相乘的结果,而分母是真分数的分母和整数的乘积。计算带分数。带分数是由一个整数和一个真分数组成的分数。
假分数化为带分数的方法是首先分子除以分母,得出来的整数做带分数的整数部分,得出的余数做分子部分,分母不变即可。假分数简介:分子大于或者等于分母的分数叫假分数,假分数大于1或等于1。分数值大于1或等于1的分数,即分子大于或等于分母的分数称假分数。
把假分数化成整数或带分数的方法
1、把假分数化成整数或带分数的方法如下:化成带分数:步骤:用假分数的分子除以分母,得到的商作为带分数的整数部分,余数作为新的分子,分母保持不变。例子:$frac{9}{4}$ 可以化为 $2frac{1}{4}$,因为 $9 div 4 = 2$ 余 $1$,所以整数部分为 $2$,分数部分为 $frac{1}{4}$。
2、把假分数化成整数或带分数的方法如下:带分数法:带分数法将假分数表示为一个整数和一个真分数的组合。以下是一个详细的步骤:假分数:a/b,将分子a除以分母b,得到商q和余数r。这可以表示为a÷b=q余r。将商q作为带分数的整数部分。将余数r作为新的分子。
3、假分数化成带分数和整数的方法如下:化成整数:当假分数的分子能被分母整除时,将分子除以分母,所得的商即为该假分数对应的整数。化成带分数:当假分数的分子不能被分母整除时,进行除法运算,所得的商即为带分数的整数部分,余数作为带分数分数部分的分子,分母保持不变。即,假分数=整数部分+。
4、把假分数化成整数或带分数的方法如下:如果分子除以分母能整除,则假分数化简为整数: 步骤:直接用假分数的分子除以分母,得到的商即为整数结果。如果分子除以分母不能整除,则假分数化简为带分数: 步骤一:用假分数的分子除以分母,得到的商作为带分数的整数部分。
5、假分数化成带分数和整数的方法:假分数化成整数或者带分数时,假分数的分子除以分母,能整除的,所得的商就是整数;不能整除时,所得的商就是带分数的整数部分,余数是分数部分的分子,分母不变。分子大于或者等于分母的分数叫假分数,假分数大于1或等于1。
6、假分数化成带分数和整数的方法如下:假分数化成整数: 当假分数的分子能被分母整除时,将分子除以分母,所得的商即为整数。假分数化成带分数: 当假分数的分子不能被分母整除时,将分子除以分母,所得的商作为带分数的整数部分; 余数作为带分数分数部分的分子,分母保持不变。
如何把假分数化成带分数或整数
1、假分数化成整数: 当假分数的分子能被分母整除时,将分子除以分母,所得的商就是该假分数对应的整数。假分数化成带分数: 当假分数的分子不能被分母整除时,进行除法运算,所得的商是带分数的整数部分; 余数则作为带分数的分数部分的分子,分母保持不变。
2、步骤:用假分数的分子除以分母,得到的商作为带分数的整数部分,余数作为新的分子,分母保持不变。例子:$frac{9}{4}$ 可以化为 $2frac{1}{4}$,因为 $9 div 4 = 2$ 余 $1$,所以整数部分为 $2$,分数部分为 $frac{1}{4}$。
3、把假分数化成整数或带分数的方法如下:如果分子除以分母能整除,则假分数化简为整数: 步骤:直接用假分数的分子除以分母,得到的商即为整数结果。如果分子除以分母不能整除,则假分数化简为带分数: 步骤一:用假分数的分子除以分母,得到的商作为带分数的整数部分。
假分数可以化成带分数吗?
1、并不是。如果题目要求假分数化成带分数,那么就需要把假分数化成带分数;反之,就不用。分子大于或者等于分母的分数叫假分数,假分数大于1或等于1。分数值大于1或等于1的分数,即分子大于或等于分母的分数称假分数。如果在整个有理数范围内讨论,则绝对值大于或等于1的分数为假分数。带分数是假分数的一种形式。一般读作几又几分之几,假分数的倒数一定不大于一。
2、假分数一定要化成带分数。带分数是假分数的一种形式。不同的书籍关于分数有不同的定义,一种观点认为阶段。等都视为分数,属于分数中的假分数 。另一种观点认为,能化成整数的分数都不是分数 。把单位“1”平均分成若干份,表示这样的一份或几份的数叫做真分数。
3、找出假分数的最简形式。即,通过约分,将假分数化成不能再简化的形式。确定假分数的分子和分母。假分数的分子是整数和真分数的分子相乘的结果,而分母是真分数的分母和整数的乘积。计算带分数。带分数是由一个整数和一个真分数组成的分数。
4、综上所述,假分数不一定要化成带分数,这取决于具体的使用场景、个人偏好以及数学运算的需求。
5、如果题目中,没有要求的话,只要是最简假分数,就不需要化成带分数。小学分数四则运算的结果是假分数的,一定要化为带分数吗?小学分数四则运算的结果是假分数的,不一定要化为带分数的,两样都可以的。
假分数化成带分数
并不是。如果题目要求假分数化成带分数,那么就需要把假分数化成带分数;反之,就不用。分子大于或者等于分母的分数叫假分数,假分数大于1或等于1。分数值大于1或等于1的分数,即分子大于或等于分母的分数称假分数。如果在整个有理数范围内讨论,则绝对值大于或等于1的分数为假分数。带分数是假分数的一种形式。一般读作几又几分之几,假分数的倒数一定不大于一。
假分数化带分数:把假分数化成整数或带分数,要用分子除以分母:能整除的,所得的商就是整数;不能整除的,商就是带分数的整数部分,余数就是分数部分的分子,分母不变。带分数注意:带分数的分数部分不能是假分数。带分数与字母相乘时要写成假分数的形式。
例如,假分数7/3,7除以3商为2余1,所以带分数为2又1/3。
假分数化为带分数方法是:用分子除以分母,所得的商做带分数的整数部分、余数做分子、分母不变。假分数的区分方法 假分数的分子比分母大或者相等,而带分数是非零整数与真分数相加所成的分数。
关于假分数怎么化成带分数的过程和假分数如何化成带分数过程的介绍到此就结束了,不知道你从中找到你需要的信息了吗 ?如果你还想了解更多这方面的信息,记得收藏关注本站。
本文可能通过AI自动登载或用户投稿,文章仅代表原作者个人观点。本站旨在传播优质文章,无商业用途。如侵犯您的合法权益请联系删除。